
Poker ile ilgili adacan tarafından düzenlenen etkinlik sayesinde bu konu hakkında edindiğim bilgileri biraz da mizah katarak siz değerli okuyucular ile paylaşmıştım. Bu konudaki araştırmalarıma devam ederek edindiğim bilgileri kaldığım yerden yazarak devam etmek istiyorum. İlk yazımda da belirttiğim gibi poker fazla bilgim olmayan bir konu. Bundan dolayı edindiğim bilgileri yorumlayarak ve biraz da mizah katarak anlatıyorum. Hatalarım olursa bu konuda bilgili arkadaşlarımızın hatalarımı düzelteceğinden eminim.
Poker hakkında bilgileri içeren ilk yazıma bu linkten ulaşabilirsiniz. Ayrıca ilk yazıda oy desteği veren nhl, btb, ufuk bey, canan hanım, adacan ve diğer tüm arkadaşlara teşekkür ederim. Poker ile ilgili bilgilere kaldığımız yerden devam edelim.
Poker Oyununda En İyi Eller ve Matematiksel Olasılıkları
Her oyunun oynanış şekline göre bir kazanış şekli vardır. Poker oyununda da oynarken kazanılması için gereken durumlar vardır. Yani oyunda en iyi elleri oluşturmamız gerekiyor. Bu en iyi eli olşturan oyuncu kazanmış olmakta. Şimdi bu ellerin durumlarını en iyisinden başlayarak sırasıyla görelim. Ve bu ellerin matematiksel olarak olma olasılıklarına bakalım.
ROYAL FLUSH

Poker sporunda karşımıza çıkan en iyi el durumudur. Bu el durumunda kazanma olasılığımız kesindir. Aynı cinsten en yüksek beş kartın bir araya gelmesine poker sporunda Royal Flush denir. En önemlisi kartların aynı cins olması gerekir. Matematiksel olarak oyunda bu durumun oluşması için dört farklı olasılık durumu vardır. Dört farklı cinsten kart çeşidi olduğu için.
STRAIGHT FLUSH

Bu el durumu; Aynı cinsten beş kartın ard arda gelme durumudur. Yani kartlarımızın numaraları ardışık olmalıdır. Yani doğal sayılarda ardışık olma durumu gibi. Örneğin; 5, 6, 7, 8 ve 9 aynı elde olması gibi. Matematiksel olarak düşünürsek bu durumun elimizde olma şartı Royal Flush a göre daha fazladır. Fakat elimizde olma olasılık oranı daha düşüktür. Sadece bir kart cinsinde Straight Flush olma olasılığı 8 durum vardır. Ayrıca dört farklı cinsten kart olduğuna göre 32 farklı durumu karşımıza çıkmaktadır.
FOUR OF A KIND

Aynı numaralı dört faklı kart değerinin yan yana gelmesi durumuna Four Of A Kind denir. Matematiksel olarak bu durumun oyunda olması için 13 durum vardır. Beşinci kart olma durumunu işin içine katmazsak. Eğer beşinci kart durumunu dahil edersek bu durumun oluşma olasılıkları artmakta.
FULL HOUSE

Oyunda bir tane çift ve bir üçlünün yan yana gelme durumuna Full House denir. Matematiksel olarak bu durumun oluşması için olasılık durumu fazladır. Şöyle bir örnek verecek olursak; Diyelim ki yukarıdaki resimde gibi çift durumu ''K-K'' ve üçlü durumu ise ''A-A-A'' şeklinde. İlk olarak üçlü durumunu bozmadan ikili durum olasılıkları var. İkinci olarak da tersi durumu ikili durumlara dokunmadan oluşabilecek üçlü durumları var. Sonunda da bunları çarparak oluşabilecek tüm durumları hesaplamış oluruz.
FLUSH

Oyunda aynı cinsten beş kartın elimizde bulunma durumuna Flush denir. Matematiksel olasığını düşünürsek; Bir cins karttan 13 tane kağıt var. Bunlardan beş tanesinin elimizde olma olasılığı ise C(13,5)=99*13=1287 dir. Bu sadece bir cins kart için geçerlidir. Dört farklı cins kart için olasılık durumu daha da artmakta.
STRAIGHT

Sırasıyla olmak koşuluyla farklı cinsten beş kartın bir elimizde olmasına pokerde Straight denir. Matematiksel olarak bu durumun oluşma olasılıkları düşünürsek;
Diyelim ki elimizde kırmızı 4 var. Bundan sonra gelmesi gereken kart 5 olmalı. Dört farklı cinsten kağıt vardı. Birini çıkardık geriye üç tane farklı cinsten kağıt var. Bunlardan bir tanesinin gelme durumu C(3,1)=3 ve on üç kart içinden de beşin gelme durumu C(13,1)=13 olur. Son olarak bunları çarparsak kırmızı dörtten sonra gelmesi gereken 5 için 39 durumdan bir tanesidir. Bunu sadece ilk iki kart için düşündük. Aynı durumları 3,4 ve 5. kartlar içinde düşünmemiz gerekir. Böylece olma olasılıkları artmakta.
THREE OF A KIND-TRIPS

Elimizdeki beş karttan üçünün aynı değerde olmasına pokerde Three Of A Kind-Trips denir. Matematiksel olasılığını düşünürsek;
Diyelimki üçlü kartlar 6 olsun. Bunun olma durumu: C(13,1)*C(13,1)*C(13,1)*C(4,3)=A çarpımından bulunur. Geriye kalan iki kart içinde: 52 karttan üçünü seçtik. Kalan kartlar 49 ve bunlardan da iki tanesini seçmemiz gerekiyor. Bu durum içinde C(49,2)=B olasılık var. Son olarak ta bu iki durumu çarpmamız gerekiyor. A*B, Three Of A Kind-Trips durumunun elimizde olma olasılığını vermekte.
TWO PAIRS

Elimizde aynı değere yani aynı numara değerine sahip iki tane durumun olmasına pokerde Two Pairs denir. Matematiksel olasılığını düşünürsek;
Diyelim ki çiftlerden birinin numarası 7 olsun. Bunun olma olasılığı C(13,1)=13. Diğer kartın farklı cisten yedi olma durumu ise C(3,1)*C(13,1)*C(13,1)=3*13=39 durum var. Bunlarıda çarparsak (13*39) ilk aynı durumun olmasını bulmuş olduk. İkinci durum içinde bunları düşünürsek olasılık durumları iyice artacaktır. Son olarak birde beşinci kartı düşünmemizde gerekiyor tabii.
ONE PAIR

Elimizde aynı değere sahip iki kartın olması durumuna One Pair denir. Two Pairs durumuna göre elimizde olma olasılığı daha yüksek bir durumdur. Olma olasılığını düşünürsek;
Diyelim ki çift olacak kart numarası 2 olsun. Bunun olması için C(4,1)*C(13,1)=A şart var. Diğer kartın farklı cinsten 2 numara olma olasığı ise C(3,1)*C(13,1)=B dir. Son olarak bu iki durumu çarparsak (A*B) bir çift olma durumunu bulmuş oluruz. Diğer üç kart durumları ise işe dahil etmedik. Onlarıda katarsak durumlar daha da artacaktır.
HIGH CARD

Elimizde her hangi cins kartlardan yüksek beş kartın bulunma durumuna pokerde High Card denir. Matematiksel olasılığı ise bu durumunda fazladır. Duruma göre değişiklik göstermektedir. Hesaplama işlemi gerçekten zor. Çok sayıda durum olduğu için hepsini tek tek düşünmemiz gerekir.
NOT: C(... , ...) gösterimi matematikteki kombinasyon işleminin gösterilişidir.
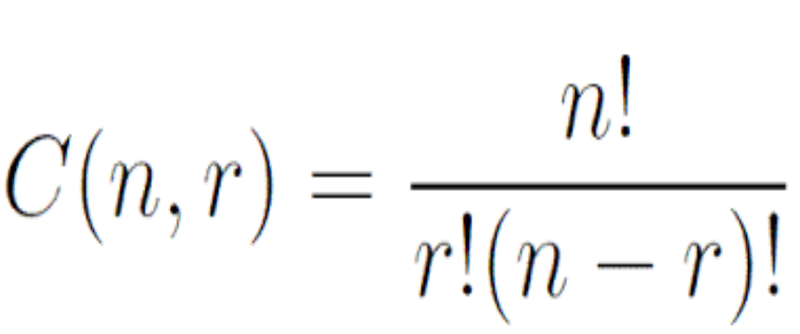
Dünyaca Ünlü Düzenlenen Poker Turnuvaları
Poker dünya üzerinde çok sayıda kişi tarafından bir oyun. Diğer oyunlarda olduğu gibi pokerde de dünya genelinde düzenlenen organizasyonlar ve turnuvalar var. Şimdi bunlardan bazıları hakkında bilgilere bakacak olursak;
World Poker Tour (WPT) - Dünya Poker Turnuvası

İlk olarak bu turnuva televizyonlardan 2003 yılında gösterilmeye başlanmıştır. Amerika Birleşik Devletleri'nde yayınlanan bir yarışmadır. Bu turnuvaya en ünlü poker oyuncuları katılmaktadır. Turnuvanın finali Amerika'da yapılmakta. Turnuvaya katılım ücreti dört bin dolardır. Elemeli turlardan geçtikten sonra final için Las Vegas'ta büyük final yapılmakta. Turnuvada dağıtılan ödül miktarı on milyon doları bulmaktadır. Finale kadar olan eleme aşamaları Kıbrıs'ta yapılmaktadır.
European Poker Tournament (EPT) - Avupa Poker Turnuvası

Bu turnuva Poker Stars tarafından düzenlenmektedir. Turnuvaya online olarak katılım yapılabilmekte. Ayrıca dünyaca ünlü poker oyuncularından bazılarıda bu turnuvaya katılmaktadır. Ayrıca bu turnuvada televizyonlardan yayınlanmaktadır.
World Series Of Poker (WSOP) - Dünya Poker Serisi

Dünya üzerinde düzenlenen en prestijli turnuvadır. Her yıl binlerce kişi bu turnuvaya katılmaktadır. Bu turnuva ilk kez 1970 yılında Las Vegas'ta yapılmış ve turnuvayı kazanan kişi Johnny Moss olmuştur.
Dünya Poker Serisi diğer turnuvalarda olduğu gibi televizyonlardan ve internetten canlı olarak yayınlanmaktadır. Binlerce kişi bu turnavaya katılmakta. Şampiyon olmak için mücadele vermektedir. Para ödülü dışında turnuvada kazanılan en büyük ödül ise WSOP yüzüğünü kazanmaktır. Futbolda futbolcular için altın top ödülü ne ise poker oyuncuları içinde WSOP yüzüğü aynı manaya gelmektedir.
WSOP Yüzüğü Kazanan Bazı Poker Oyuncuları

WSOP yüzüğünü kazanan ilk kişi 1970 yılında turnuvayı birinci bitiren Johnny Moss (Yukarıdaki resimde yer alan yaşlı amcamız) ve en son 2018 yılında düzenlenen turnuvayı kazanan kişi ise John Cynn olmuştur. Bu iki isim dışında yüzüğü kazanan diğer bir kaç isim ise şöyle; Doyle BRUNSON, Johnny CHAN, Noel FURLONG, Martin JACOBSON gibi isimler.
Poker hakkında bilgiler içeren yazı serimin ikincisini burada bitirmek istiyorum. Umarım faydalı olmuştur. İlerleyen zamanlarda umarım yazı serime devam edebilirim. Son olarak konu hakkındaki yorumlarınızı bekliyorum.
Yorumlar